▷광학의 거울 시스템◁
-Mirror Image formation & Mirror convection & Mirror formula & Power notation-
렌즈의 광학 시스템에서 볼록과 오목에서의 초점, 이미지 형성원리에 대해 글을 썼었다.
이 부분에 대해서 알고있다는 가정하에 이번에는 거울에서 살펴보도록 하겠다.
혹시 초점을 찾는방법을 모른다면 다음 글을 참고하길 바란다.
↓↓
2020/06/01 - [꿀나리의 광학 이야기 ★] - 볼록렌즈와 오목렌즈의 초점과 초점거리_Focal point and Focal length
볼록렌즈와 오목렌즈의 초점과 초점거리_Focal point and Focal length
▷볼록렌즈와 오목렌즈의 초점과 초점거리◁ -Convex and Concave focal_point and focal length - 이번에는 기하광학에서 렌즈와 관련하여 빛의 진행방향을 파악하기 위한 기본과 표시법, 물체와 이미지 형��
kkulnari.tistory.com
< Spherical Mirror In Oprics >
다음 그림은 오목거울(Concave Mirror)과 볼록거울(Convex Mirror)의 광학 시스템이다.
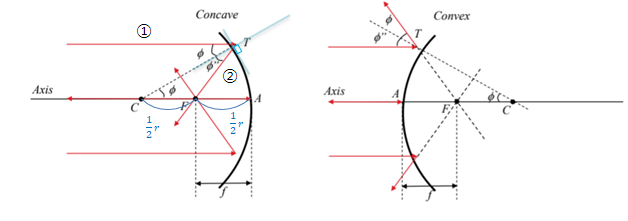
렌즈와 달리 거울은 빛을 반사시키는 특성이 있기 떄문에 빛의 진행과정에 차이가 있다.
Concave 거울의 경우, 평행하게 입사하는 ①번 빛이 거울의 표면에서 반사된 후,
표면과 수직한(법선)에 대하여 \(\phi'\)의 각을 갖고 반사되고, 광축과 만나는 점에 초점(Focal point : F)이 생긴다.
이 때, \(\phi\)와 \(\phi'\)는 반사의 법칙(Law of reflection)에 의해 \(\phi'=\phi\) 관계임을 알 수 있다.
그러면 반사법칙에 의한 \(\phi\)와 엇각에 의한 \(\phi\)로인해 △TCF는 CF=FT인 이등변 삼각형이된다.
이에, 근축 광선을 활용하게되면 ( \(\phi<<1\) ), FT는 FA로 달라붙게되어 다음의 관계를 형성한다.
\(FA=\frac{1}{2}CA\)
FA는 초점거리(Focal length : f)에 해당하고, CA는 반지름r이므로 다음과 같이 나타낼 수 있다.
\(f=-\frac{1}{2}r\)
( A에서 쟀다고 생각하여 (-)부호가 붙었다. )
< Image formation in mirror >
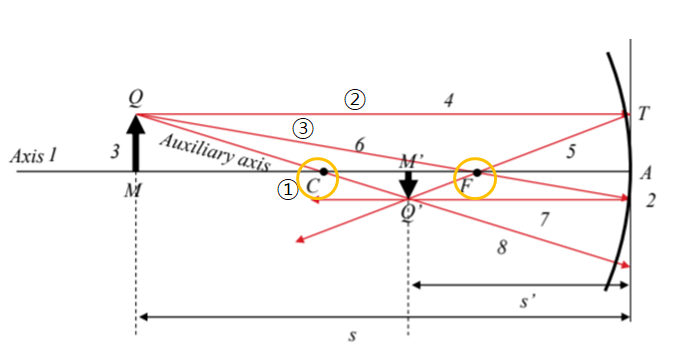
거울의 ①,②,③ 광선은 렌즈의 경우과 똑같이 다음의 특성들로 빛이 모이는 지점을 찾을 수 있다.
①번 광선 : center C를 지나는 점은 똑바로 진행한다.
②번 광선 : 평행하게 입사하는 빛이 거울의 표면에서 반사 후, 광축과 만나는 점이 초점이다.
③번 광선: 초점을 지나는 빛이 거울 표면에서 반사 후, 평행하게 진행한다.
이를 통해서, 물체(Object)의 한 점Q는 거울 표면에서 반사 후, Image의 한 점 Q'으로 모이는 것을 확인할 수 있다.
이 때, 형성된 이미지 M'Q'은 도립 & 실상 형태이다. ( Inverted and Real )
< Mirror Sign Convection >
1.왼쪽에서 오른쪽으로 거리를 측정하면 (+), 오른쪽에서 왼쪽으로 거리를 측정하면 (-)이다.
2. 입사광선은 왼쪽에서 오른쪽으로 진행하고, 반사광선은 오른쪽에서 왼쪽으로 진행한다.
3. 초점거리(Focal length)는 초점(Focal point)에서 vertex로 측정된다. 이 조건에서 concave mirror는 (+) convex mirror는 (-)로 측정된다.
4. 반지름 r은 vertex에서 center C(center of curveture)로 측정된다. 이 때, Concave Mirror는 r<0 (negative) Convex Mirror는 r>0 (positive)로 측정된다.
< Mirror Formula >
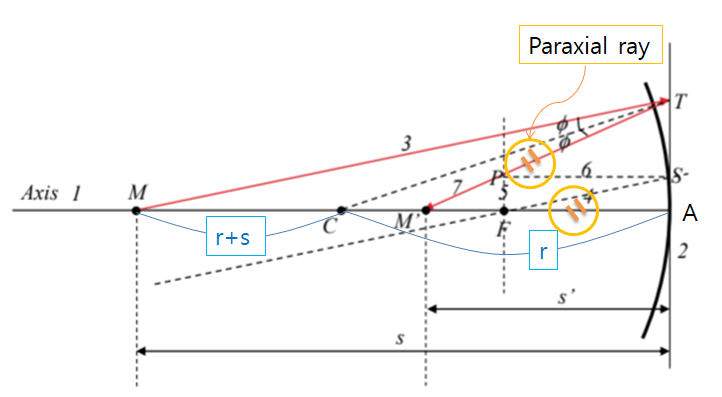
*주의 : MC가 r+s로 표현된 것은, r<0이기 때문에 더해줘야 빼기가 되기 때문이다.
먼저, Proportionality에 의해서 다음의 관계를 찾을 수 있다.
(1). \(\frac{MC}{MT}=\frac{CM'}{M'T}\)
앞서 진행했던 방법과 같이, 근축 광선을 적용하면 다음 식을 얻는다.
(2). for paraxial rays : \(MT \approx MA=s\) and \(M'T \approx M'A=s'\)
\(MC\)와 \(CM'\)도 초점거리와 반지름에 대한 식으로 정리해준다.
(3). \(MC=MA-CA=s+r\) and \(CM'=CA-M'A=-(r+s')\)
이제, \(\frac{MC}{MT}=\frac{CM'}{M'T}\)를 앞서 구한 관계식을 이용하여 정리하면 다음의 결과를 얻을 수 있다.
(4). \(\frac{s+r}{s}=-\frac{s'+r}{s'}\)
한 번 더, 정리해주면 광학 거울에서 사용하는 Mirror formula를 구할 수 있다.
Mirror formula : \(\frac{1}{s}+\frac{1}{s'}=-\frac{2}{r}=\frac{1}{f'}\)
거울에서 배율(magnification)도 렌즈와 같이 Object와 Image의 비율로 구할 수 있다.
Magnification : \(m=\frac{y'}{y}=-\frac{s'}{s}\)
< Power of the mirror >
거울에서도 렌즈와 같은 표기법을 사용한다.
이 표기법을 처음본다면 렌즈에서 정리했던 부분을 참고하도록 하자. (하단에 위치한다.)
↓↓
2020/06/03 - [꿀나리의 광학 이야기 ★] - 렌즈 공식 유도_Derivation of the lens formula_Thin lens_Power notation
렌즈 공식 유도_Derivation of the lens formula_Thin lens_Power notation
▷Derivation of the lens formula◁ -렌즈 공식 유도- 이번 글은 Thin lens에 대한, 렌즈 공식과 렌즈 제작자 공식(lens makers' formula), 2가지에 관하여 알아볼 것이다. 가우시안 공식(Gaussian formula)과 Co..
kkulnari.tistory.com
n=1, 공기중이라는 가정하에서 다음 관계를 정리하였다.
1. \(P=\frac{1}{f}\)
2. \(V=\frac{1}{s}\) and \(V'=\frac{1}{s'}\)
3. \(K=\frac{1}{r}\)
위 식과 Mirror formula의 식을 이용하면 \(V+V'=\frac{1}{s}+\frac{1}{s'}=-\frac{2}{r}\)에 의해 4번 식을 얻는다.
4. \(V+V'=-2K\) and \(V+V'=P\)
\(P\) 또한 마찬가지로 Mirror formula \(-\frac{2}{r}=\frac{1}{f}\)에 의해 5번 식을 얻는다.
5. \(P=-2K\)
6. \(m=\frac{y'}{y}=-\frac{V}{V'}\)
Power의 단위는 Diopter이며, 거리요소가 m로 측정되었을 때이다.
광학에서의 거울 시스템, 거울 공식_Spherical Mirror in optics_Mirror formula
'꿀나리의 광학 이야기 ★' 카테고리의 다른 글
| 비네팅 현상은 왜 나타날까?_Vignetting In Optics (0) | 2020.06.08 |
|---|---|
| 거울의 구면수차_Mangin and Paraboloidal mirror (0) | 2020.06.07 |
| Field Stop과 Aperture Stop은 무엇일까?_FOV와 광학 조리개에 대하여 (1) | 2020.06.05 |
| 카메라의 f number에 대해서_f/#_f/stop (0) | 2020.06.04 |
| 렌즈 공식 유도_Derivation of the lens formula_Thin lens_Power notation (0) | 2020.06.03 |



