▷Conjugate points and planes◁
-가우시안 공식_Gaissian Formula_배율_Magnification-
가우시안 공식과 배율을 확인하기 앞서 Conjugate points와 planes의 관계를 확인해보자.
이들의 대칭성을 통해 관계식을 도출할 수 있기 때문이다.
< Conjugate points and planes >
Conjugate point라 하면 광학에서는 켤레점 또는 공액점이라고 한다.
하나의 물점(Object point)에서 나온 빛이 광학기기를 통과하여 상점(Image point)에 맺힐 때
두 개의 점을 conjugate points, 두 개의 면을 conjugate planes라고 한다.
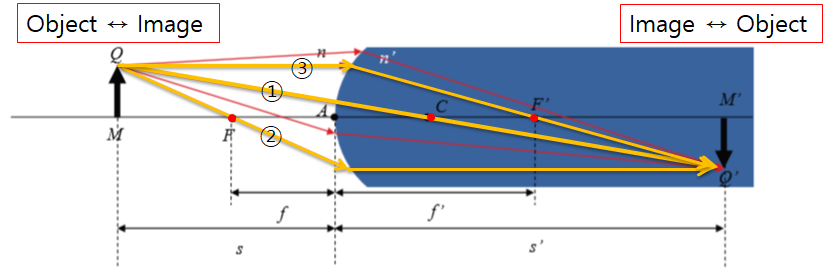
이전에 이미지 형성과정에 대해 위 그림을 이용해서 ①,②,③번 광선으로 설명한 적이 있었다.
그때 왼쪽에 Object를 두었고 오른쪽에 Image가 형성되는 그림이었다.
위 그림은 둘의 위치가 서로 바뀔 수 있다는 것을 알려준다. 즉, 오른쪽에 Object, 왼쪽에 Image가 형성될 수 있다.
이는 대칭성에 관한 이야기로서 서로의 역할을 맞바꿀 수 있는 관계임을 의미한다.
위에서 설명한 Object, Image의 점 M과 M'의 관계를 Conjugate points,
물체가 놓인 면 Object plane과 이미지가 형성되는 면, Image plane의 관계를 Conjugate plane이라고 한다.
그러면 이러한 이미지의 점(Point)과 크기(size)를 어떻게 정할까?
이 방법에는 작도법으로 그리거나 실험적인 방법이 있겠지만, 가우시안 공식(Gaussian formula)을 이용해보려 한다.
< Gaussian Formula : 가우시안 공식 >
일단 가우시안 공식은 다음과 같이 생겼고, 이 공식이 어떻게 나온 것인지 살펴보려고 한다.
\(\frac{n}{s}+\frac{n'}{s'}=\frac{n'-n}{r}\)
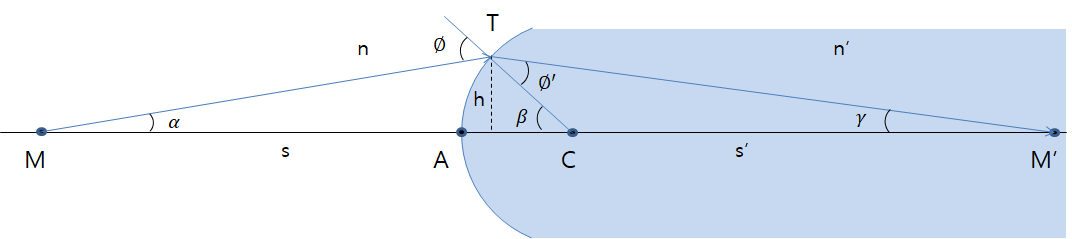
위 그림은 계속 살펴보았던, MQ 물체와, M'Q'의 이미지 관계에서 M과 M'의 관계를 나타낸 그림이다.
굴절에서는 잊을 수 없는 스넬의 법칙 (Snell's law)를 사용하여보자.
1. 스넬의 법칙 (근축광선) : \(\frac{\phi}{\phi'}=\frac{n'}{n}\)
2. 삼각형 MTC : \(\phi=\alpha+\beta\) (외각 관계로부터 나온 식이다.)
3. 삼각형 TCM' : \(\phi'=\beta-\gamma\)
4. 2번, 3번에서 구한 식을 1번 \(\phi\)와 \(\phi'\)에 대입해준다.
그러면 다음과 같이 정리할 수 있다.
5. \(n'\beta-n'\gamma=n\alpha+n\beta\) 또는 \(n\alpha+n'\gamma=(n'-n)\beta\)
6. \(\alpha,\beta,\gamma\)에 근축광선(Paraxial rays)을 오른쪽 식에 적용해보자.
먼저, \(\alpha\)를 근축 근사 하면 \(tan\alpha \approx \alpha \approx \frac{h}{s}\)가 되고,
\(\beta\) 와 \(\gamma\)도 똑같이 적용하여 식에 대입하여 정리해준다.
----> \(n\alpha+n'\gamma=(n'-n)\beta \approx n\frac{h}{s}+n'\frac{h}{s'}=(n'-n)\frac{h}{r}\)
이를 다시 한번 정리해주면 최종적으로 다음과 같은 관계식을 얻을 수 있다.
가우시안 공식(Gaussiam Formula) : \(\frac{n}{s}+\frac{n'}{s'}=\frac{n'-n}{r}\)
위에서 살펴본 가우시안 공식을 Conjugate points와 planes관계에 적용하면 가우시안 공식을 초점에 관한 식으로
정리할 수 있고, 초점과 거리를 활용하여 대략적인 위치를 파악할 수 있게 된다.
1. 물체(Object)가 초점 F에 있을 때 (이 말은 곧 굴절 후 광선이 평행하게 진행되며 이미지 거리(Image distance)가 무한대임을 뜻한다.)
따라서 \(s'=\infty\)을 가우시안 공식에 적용하면 다음의 식을 얻는다.
\(\frac{n}{s}+\frac{n'}{\infty}=\frac{n'-n}{r}\) ---------> \(\frac{n}{f}=\frac{n'-n}{r}\)
2, 비슷한 방식으로 이미지에 적용하면 다음과 같이 정리된다.
\(s=\infty\) ---------> \(\frac{n}{\infty}+\frac{n'}{s'}=\frac{n'-n}{r}\)
\(\frac{n'}{f'}=\frac{n'-n}{r}\)
그림으로 보면 이해하기 쉽다.
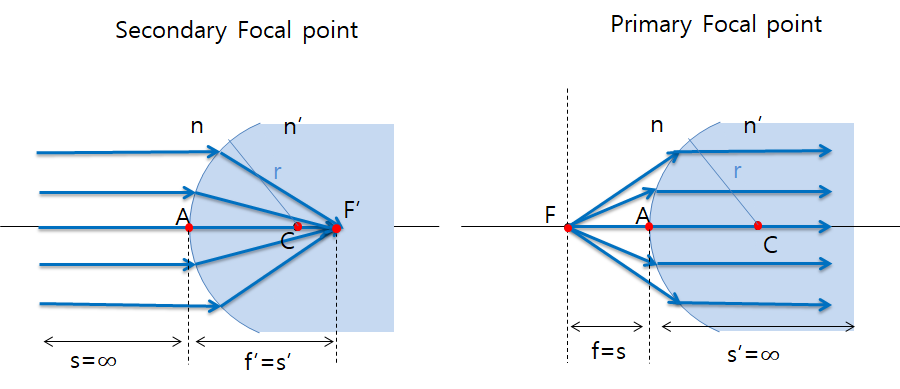
초점 위치에 물체가 있다고 하였기 때문에 초점과 물체의 거리 f=s가 같게 되고 이미지의 경우에는 f'=s'가 된다.
앞서 구한 두 식 \(\frac{n}{f}=\frac{n'-n}{r}\), \(\frac{n'}{f'}=\frac{n'-n}{r}\)으로부터 다음의 관계를 얻는다.
\(\frac{n'}{f'}=\frac{n}{f}=\frac{n'-n}{r}\)
이를 가우시안 공식에 적용하면 최종적으로 정리된 다음의 식을 얻을 수 있다.
\(\frac{n}{s}+\frac{n'}{s'}=\frac{n}{f}=\frac{n'}{f'}\)
이 식을 통해서 매질의 굴절률과 초점 또는 매질의 굴절률과 거리에 관한 정보만 있으면,
초점 또는 거리를 구함으로써 대략적인 위치를 파악할 수 있게 된다.
이번 포스팅의 마지막, 배율(Magnification)에 관한 이야기이다.
배율은 물체와 이미지의 크기에 관한 비율이라고 생각하면 된다.
< Magnification >
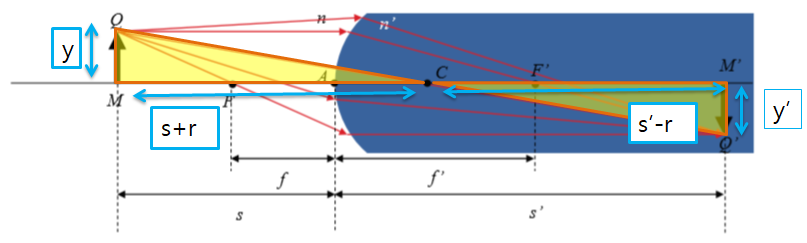
계속 봐왔던 그림이라 이젠 익숙할 것 같다.
이들은 Conjugate 관계에서 살펴보았듯 대칭성을 이루고 있기 때문에 두 개의 닮음 삼각형 MCQ와 M'CQ'을 이용해보자.
삼각형 닮음비에 의해 길이 관계를 다음과 같이 나타낼 수 있다.
\(\frac{M'Q'}{MQ}=\frac{CM'}{CM}\) ------> \(\frac{-y'}{y}=\frac{s'-r}{s+r}\)
이때, y'에 (-) 부호는 이미지가 축을 기준으로 아랫방향에 위치하기 때문이다. (y'<0)
배율은 MQ와 M'Q' 크기의 비율이므로 배율(magnification) \(m=\frac{y'}{y}=-\frac{s'-r}{s+r}\)이 된다.
이때, m이 (+) 부호, 즉 Positive이면 허상 & 정립 이미지를 얻게 된다. (Virtual and Erect)
반대로 m이 (-) 부호이면, 즉 Negative이면 실상 & 도립 이미지를 얻는다. (Real and inverted)
부호에 관한 내용이나, 이미지 형성에 대해서 잘 이해가 안 된다면 이전 글을 참고하도록 하자!
↓↓
2020/06/01 - [꿀나리의 광학 이야기 ★] - 볼록렌즈와 오목렌즈의 초점과 초점거리_Focal point and Focal length
볼록렌즈와 오목렌즈의 초점과 초점거리_Focal point and Focal length
▷볼록렌즈와 오목렌즈의 초점과 초점거리◁ -Convex and Concave focal_point and focal length - 이번에는 기하광학에서 렌즈와 관련하여 빛의 진행방향을 파악하기 위한 기본과 표시법, 물체와 이미지 형��
kkulnari.tistory.com
가우시안 공식_배율_Gaussian Formula_Magnification_Conjugate points and planes
'꿀나리의 광학 이야기 ★' 카테고리의 다른 글
| 카메라의 f number에 대해서_f/#_f/stop (0) | 2020.06.04 |
|---|---|
| 렌즈 공식 유도_Derivation of the lens formula_Thin lens_Power notation (0) | 2020.06.03 |
| 볼록렌즈와 오목렌즈의 초점과 초점거리_Focal point and Focal length (0) | 2020.06.01 |
| 확산 광선_Divergent rays_Reflection and Refraction (0) | 2020.05.31 |
| 프리즘에 의한 굴절_편차각 계산하기_Refraction by a Prism (0) | 2020.05.30 |



