▷프리즘에 의한 굴절 편차각 계산◁
-Refraction by prism and deviation angle-
이번에는 프리즘에 빛이 입사하였을 때 꺾여서 빛이 빠져나갈 때 생기는 편차각에 대해 수식으로 계산해볼 것이다.
< Refraction by Prism >
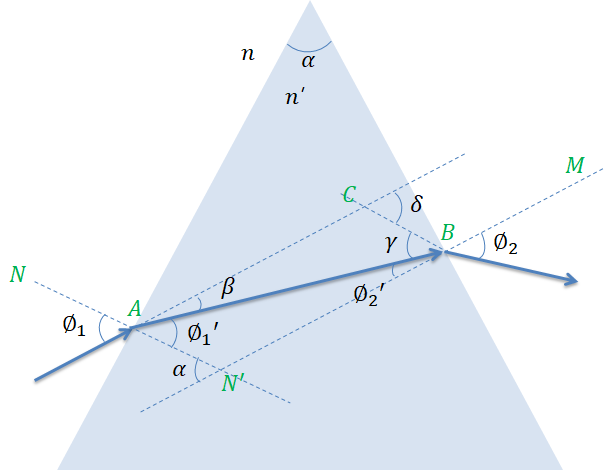
단색광 (monochromatic light)의 빛이 프리즘을 통과하였을 때 편차각(빗나가는 각)을 다음과 같이 계산할 수 있다.
1) 스넬의 법칙에 의해 다음 식을 형성할 수 있다.
\(\frac{sin\phi_{1}}{sin\phi_{1}'}=\frac{n'}{n}=\frac{sin\phi_{2}}{sin\phi_{2}'}\)
2) 첫 번째 면 (왼쪽 측면)에서 발생하는 편차각 (Deviation angle) 은 \(\beta=\phi_{1}-\phi_{1}'\) 이 된다.
3) 두 번째 면 (오른쪽 측면)에서 발생하는 편차각은 \(\gamma=\phi_{2}-\phi_{2}'\) 이 된다.
4) 전체 편차각 (Total angle of deviation)을 계산할 수 있다.
\(\delta=\beta+\gamma=\phi_{1}-\phi_{1}'+\phi_{2}-\phi_{2}'=\phi_{1}+\phi_{2}-\alpha\)
선이 많아서 헷갈릴 수 있는데, 법선 기준만 잘 찾으면 스넬의 법칙을 사용하여 어렵지 않게 계산할 수 있다.
< Minimum Deviation >
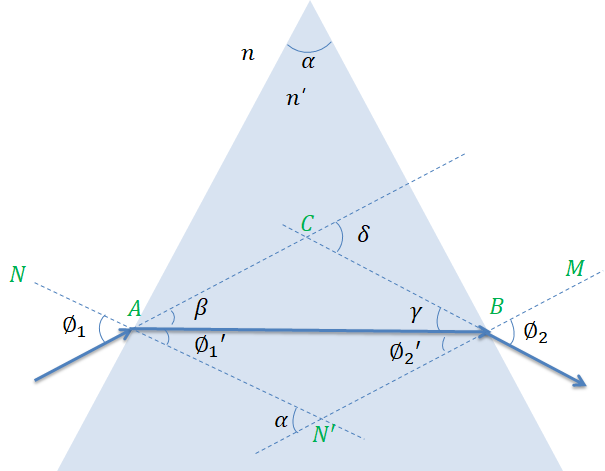
위 그림은 첫 번째 그림에서 편차각, 즉 벗어나는 각이 최소가 되는 상황이다.
편차가 최소가 되는 각 (the angle of minimum deviation)을 \(\delta_{m}\) 이라고 하자.
편차가 최소가 되어 좌우가 대칭성으로 같다고 놓으면 다음과 같은 관계를 쓸 수 있다.
\(\phi_{1}=\phi_{2}\) , \(\phi_{1}'=\phi_{2}'\) , \(\beta=\gamma\)
그러면 삼각형 두 개가 눈에 보일 것이다. ( ABC, ABN' )
위아래 같은 삼각형이 될 것이고 \(\alpha=2\phi_{1}'\)의 관계를 찾을 수 있다.
동시에 \(\delta_{m}=2\beta\) 와 \(\phi_{1}=\phi_{1}'+\beta\) 관계도 찾을 수 있다.
\(\alpha=2\phi_{1}'\) -----> \(\phi_{1}'=\frac{1}{2}\alpha\)
\(\delta_{m}=2\beta\)와 \(\phi_{1}=\phi_{1}'+\beta\) 식에서 -----> \(\phi_{1}=\phi_{1}'+\frac{\delta_{m}}{2}\)
따라서 \(\phi_{1}=\frac{1}{2}(\alpha+\delta_{m})\) 을 얻을 수 있다.
이 식들을 스넬의 법칙에 의해 정리하면 최소 편차각에 대한 관계식을 다음과 같이 쓸 수 있다.
\(\frac{sin\phi_{1}}{sin\phi_{1}'}=\frac{n'}{n}=\frac{sin\phi_{2}}{sin\phi_{2}'}\) ------> \(\frac{n'}{n}=\frac{sin\frac{1}{2}(\alpha+\delta_{m})}{sin\frac{1}{2}\alpha}\)
< Thin prism >
앞서 살펴본 프리즘의 최소 편차각을 아주 얇은 프리즘 (thin prism)이라고 생각하였을 때, 다음과 같이 근사할 수 있다.
\(\frac{n'}{n}=\frac{sin\frac{1}{2}(\alpha+\delta_{m})}{sin\frac{1}{2}\alpha}\approx\frac{\alpha+\delta_{m}}{\alpha}\)
그리고 이 프리즘이 공기중에 있다면 편차각은 \(\delta=(n'-1)\alpha\) 가 된다.
이전에 '디옵터 (Diopter)'에 대한 글을 포스팅하면서 디옵터를 프리즘에 관하여 정의 내린 적이 있었다.
↓↓
2020/05/16 - [꿀나리의 광학 이야기 ★] - 렌즈의 디옵터란 무엇일까?_디옵터와 시력 척도
렌즈의 디옵터란 무엇일까?_디옵터와 시력 척도
▷렌즈 디옵터 편◁ -렌즈의 디옵터란 무엇일까?- - 디옵터의 의미 - 내가 기하광학을 배웠을 때 접했던 디옵터의 의미는 이러했다. The displacement x in centimerters at a distance of 1m gives the power of..
kkulnari.tistory.com
위 포스팅에서 사용했던 그림이다. 왼쪽에 파란색이 Thin prism이다.
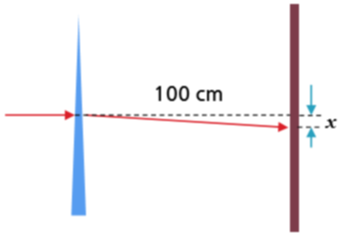
위 그림은 1 프리즘 디옵터의 힘을 가진 프리즘은 1m 떨어진 곳에서 1cm 꺾인다는 의미이다.
즉 1 diopter는 1m 떨어진 곳에서 1cm 꺾이는 것이다.
< Risley prism >
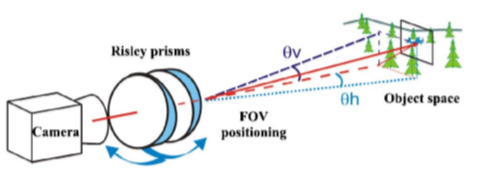
리즐리 프리즘 (Risley prism)은 같은 힘을 가진 두 개의 thin prism을 서로 반대방향으로 회전하여 결합한 것이다.
그림을 보면 삼각형 비슷한 모양이 왼쪽은 위로, 오른쪽은 아래로 향한 것을 볼 수 있다.
이렇게 두 개의 얇은 프리즘이 결합하게 되면, 첫 번째 프리즘을 통과한 빛이 두 번째 프리즘을 통과하면서
편차가 한 번 더 생기게 된다.
이를 최종 편차를 합성함으로써 수식적으로 계산할 수 있으며 다음과 같이 표현할 수 있다.
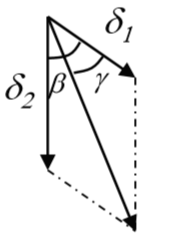
위 그림에서 Resley로 인해 생긴 deviation \(\delta\) 는 합성 값으로 \(\beta\)가 두 프리즘의 사잇각일 때
다음과 같은 관계를 얻을 수 있다.
\(\delta=\sqrt{\delta_{1}^{2}+\delta_{2}^{2}+2\delta_{1}\delta_{2}cos\beta}\)
Risley prism의 경우 \(\gamma=\frac{\beta}{2}\)의 관계에서
\(tan\gamma=\frac{\delta_{2}sin\beta}{\delta_{1}+\delta_{2}cos{\beta}}\) 의 관계식도 얻을 수 있다.
Risley prism은 프리즘의 특성으로 FOV (Field of View)를 조정함으로써
beam-steering이나 양안 조절 (binocular accommodation)에 유용하게 활용된다.
프리즘에 의한 굴절_편차각 계산하기_Risley Prism_기하광학
'꿀나리의 광학 이야기 ★' 카테고리의 다른 글
| 볼록렌즈와 오목렌즈의 초점과 초점거리_Focal point and Focal length (0) | 2020.06.01 |
|---|---|
| 확산 광선_Divergent rays_Reflection and Refraction (0) | 2020.05.31 |
| 외부 반사와 내부 반사_임계각과 전반사_Lummer-Brodhun cube (0) | 2020.05.29 |
| 색 분산_Color dispersion_프라운호퍼 선_Fraunhofer lines (0) | 2020.05.28 |
| 반사와 굴절_ Reflection and Refraction_작도법_기하광학 (0) | 2020.05.27 |



