▷Ray tracing formula◁
이전에 꿀나리 블로그에 올린 광학 관련 글을 보면, 근축광선(Paraxial ray)을 적용했었다.
근축광선을 적용하면 이미지의 위치와 크기를 비교적 간단한 방법으로 계산이 가능했기 때문이다.
하지만 실제 시스템에서는 대부분의 렌즈 aperture가 너무 커서 근축광선은 아주 작은 부분만을 구성하게 된다.
이번 글은 근축이 아닌 광선, Oblique ray를 통해 Ray tracing formula를 유도하는 것이 목적이다.
<Ray tracing formula>
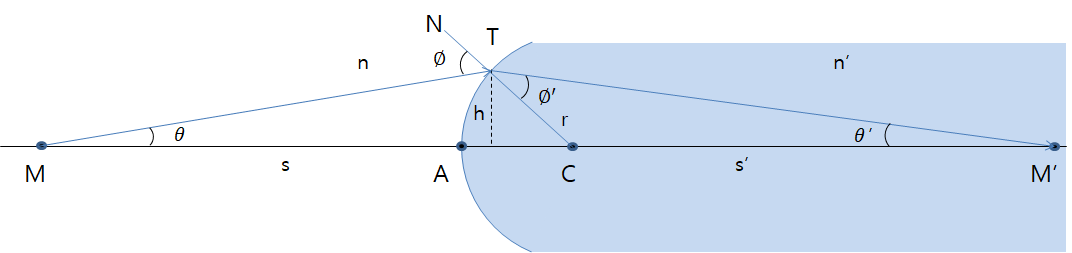
위 그림을 살펴보기 전에 각도의 표시법을 확인하도록 하자.
-각도의 표시법(Signs of the angles)-
먼저, 경사각(Slope angle)은 축에서 \(\frac {\pi}{2}\) 보다 작은 각도를 통해 반시계 방향으로 회전할 때 양의 부호를 갖는다. (Positive, +)
입사각과 굴절각은 표면 반경에서 \(\frac {\pi}{2}\) 보다 작은 각도를 통해 반시계 방향으로 회전할 때 양의 부호를 갖는다. (Positive, +)
위 그림에서 기준 조건의 반시계 반향으로 회전하기 때문에 \(\theta,\phi,\phi'\)은 양(Positive)의 부호를 갖는다.
\(\theta'\)은 기준 조건의 시계방향으로 회전했기 때문에 음(Negative)의 부호를 갖는다.
위 그림에서 아래와 같이 6개의 방정식을 얻을 수 있다.
(1). \(sin\phi=\frac {r+s}{r} sin\theta\)
(2). \(sin\phi'=\frac {n}{n'} sin\phi\)
(3). \(\theta'=\phi'+\theta-\phi\)
(4). \(s'=r-r\frac {sin\phi'}{sin\theta'}\)
(5). \(sin\phi=\frac {h}{r}\)
(6). \(\theta'=\phi'-\phi\)
(1) 번식부터 차례대로 확인해보자.
먼저, △MTC에서 \(\frac {sin\theta}{r}=\frac {sin(\pi-\phi)}{s+r}\)의 관계식을 얻을 수 있다.
이 관계식을 정리하면 (1). \(sin\phi=\frac {r+s}{r} sin\theta\) 식을 얻게 된다.
(2) 번식은 빠지면 섭섭한, 스넬의 법칙(Snell's law) \(\frac {n}{n'}=\frac {sin\phi'}{sin\phi}\)을 적용하면 \(sin\phi'=\frac {n}{n'} sin\phi\)을 어렵지 않게 구할 수 있다.
(3) 번식을 구하기 위해 ∠TCM=\(\alpha\)라고 놓도록 하겠다. 그러면 삼각형에서 각도의 특성을 활용하여 다음의 관계식을 구할 수 있다. \(\theta'+\phi'+\alpha=\pi\), \(\alpha=\pi-\phi+\theta\)
\(\alpha\)에 관한 식으로 나타냈기 때문에 \(\theta'\)에 대하여 정리함으로써 \(\theta'=\phi'+\theta-\phi\)을 구할 수 있게 된다.
이때, \(\theta'\)은 각도의 표시법에서 음의 부호였던 점을 유의하자.
(4) 번식은 (1) 번과 마찬가지로 △TCM'에서 유도할 수 있기 때문에 생략하도록 하겠다.
(5) 번식은 (1) 번식을 h에 대하여 정리한 것이다.
(6) 번식은 (3) 번식에서 \(\theta=0\) 일 때, 즉 평행 입사광이 일어날 때 상황에 대한 관계식이다.
(6) 번식을 이전에 근축광선을 사용했을 때는 \(sin\theta'=sin\phi'-sin\phi\)의 형태였었다.
실제 시스템에서 적용하면 이 부분이 (6) 번식과 같이 \(\theta'=\phi'-\phi\) 형태로 쓰이는 것을 확인해보았다.
이렇게 Ray tracing formula 총 6개를 정리해보았다.
식만 정리하면 좀 아쉽기 때문에 근축광선과 비교하여, 위 식들이 적용된 다음의 예시를 통해 학습해보도록 하자.
< Example >
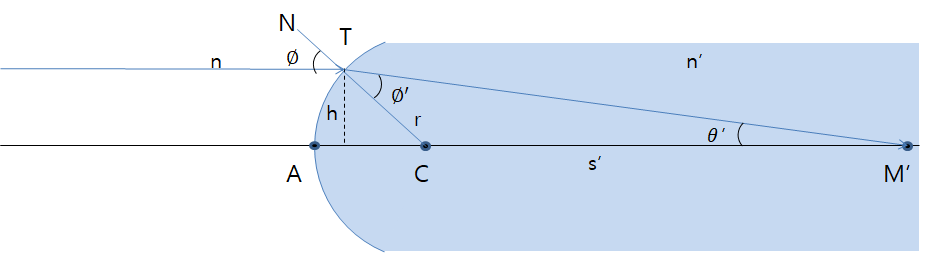
조건 : Convex spherical surface r=+5.0 cm, n'=1.67200.
위 그림과 같이 입사광이 축과 평행하게 입사하는 평행광이라고 가정했을 때, 광선의 높이를 3cm, 2cm, 1cm, 0로 설정하여 확인해보자.
아래 표를 보면, 높이에 따라 6개의 방정식에 필요한 값들이 나와있다.
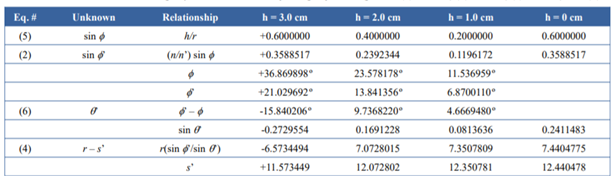
첫 번째 확인할 것은 h가 0에서 3으로 갈수록 Image distance s'이 차이가 발생한다는 것이다.
즉, h=0에서 높이가 높아질수록 근축광선을 적용하여 계산했던 렌즈 공식과 차이가 생기게 된다.
위 표는 실제 시스템에서 적용한 Ray tracing formula를 적용한 값들이지만, h=0에서 또는 근처에서는 근축광선을 다룰 수 있기 때문에 근축광선의 formula를 적용할 수 있다.
즉, Real system에서 (6) 번의 \(\theta'=\phi'-\phi\)식을, 근축광선 \(sin\theta'=sin\phi'-sin\phi\)식으로 쓸 수 있다.
h=0의 경우에서 다른 열에서 \(sin\phi\) 값 중 하나에 해당하는 숫자를 선택해보자.
꿀나리는 h=3.0cm를 선택해보겠다.
h=3.0cm일 때, \(sin\phi\) 값은 +0.60000000이고, \(sin\phi'\) 값은 +0.3588571이다. (표에서 확인할 수 있다.)
이 두 값의 차를 구하면 0.2411483이다.
따라서 근축광선은 식에 적용하면 \(sin\theta'=0.2411483\) 을 얻을 수 있다.
h=0의 (4) 번 값을 구하기 위해서 +0.3588571에 5를 곱하고 0.2411483으로 나누어준다. ( 4번 방정식은 r을 곱하고 \(sin\theta'\)으로 나눈 값이기 때문이다.)
마지막으로 s'을 구하기 위해 r을 더하면 h=0에서 s'=12.440478 값을 근축광선을 적용하여 구할 수 있게 된다.
이번 글은 surface 1개에 대한 ray tracing formula를 확인해보았다.
다음 글에서는 오늘 구한 공식을 2개의 surface에 적용하여 ray tracing formula를 확인해보려고 한다.
'꿀나리의 광학 이야기 ★' 카테고리의 다른 글
| LED 특성을 나타내는 기본 용어 정리 (0) | 2020.06.13 |
|---|---|
| Ray tracing and paraxial ray formula_두번째 이야기_공식모음 (0) | 2020.06.11 |
| 비네팅 현상은 왜 나타날까?_Vignetting In Optics (0) | 2020.06.08 |
| 거울의 구면수차_Mangin and Paraboloidal mirror (0) | 2020.06.07 |
| 광학에서의 거울 시스템, 거울 공식_Spherical Mirror in optics_Mirror formula (0) | 2020.06.06 |


